Autres fiches de statistique

Un test, qu’il soit statistique ou pas, consiste à vérifier une information hypothétique.

En statistique mathématique :

• l’information hypothétique concerne la population à laquelle on s’intéresse. C’est une information statistique qui peut être :

Une distribution qu’une variable d’intérêt quelconque est censée présenter, par exemple une loi de Gauss.
Une valeur ponctuelle à laquelle une statistique, par exemple une moyenne, une fréquence, etc. serait égale (on qualifie une telle valeur d’hypothèse simple).
Un intervalle de valeurs auquel appartiendrait la valeur d’une statistique, comme ci-dessus (on qualifie un tel intervalle d’hypothèse composite).
L’indépendance statistique de deux variables.

Un test statistique permet de vérifier le succès (ou l’échec) d’une action entreprise pour modifier la valeur d’une statistique de population. Exemples :
- On cherche à augmenter le nombre moyen des clients servis à l’heure, qui est actuellement de = 10.
- On cherche à faire tomber la proportion p_pop des appareils défectueux en dessous de 3%.

• La vérification de l’hypothèse par un recensement de la population est remplacée par l’observation de la valeur d’une statistique dans un échantillon de taille n prélevé au hasard ou par d’autres méthodes aléatoires.
  On compare cette valeur à celles auxquelles on pouvait s’attendre si l’hypothèse est vraie. La distribution des probabilités de n’importe quelle statistique d’échantillon aléatoire peut se représenter schématiquement comme se représente dans le premier exemple ci-dessus la distribution de la moyenne d’un échantillon de taille n en faisant l’hypothèse que l’action a été un échec, et que le nombre moyen de clients est resté égal à = 10 :



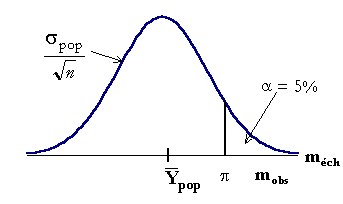
On "voit" que, si l’hypothèse est vraie, il y a une forte probabilité d’observer une valeur de la statistique proche de son espérance mathématique, dans l’exemple ci-dessus une moyenne d’échantillon proche de la moyenne hypothétique dans la population.

• Si au contraire la valeur observée pour la statistique présente un écart important avec l’espérance mathématique des valeurs attendues avec l’hypothèse envisagée, c’est-à-dire qu’elle tombe dans un intervalle où elle n’avait qu’une probabilité faible de se produire, au delà du seuil p qui n’a que 5% des chances d’être dépassé, dans le schéma ci-dessus, on est en droit de considérer que cette observation est en réalité proche de l’espérance mathématique d’une hypothèse alternative à celle envisagée :

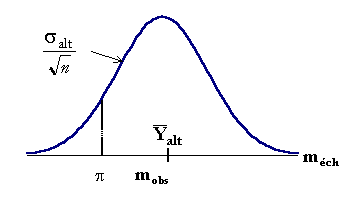
Mais on "rejette" alors comme fausse l’hypothèse avec un risque certain risque qui doit évidemment être faible, et qui est d’autant plus faible que l’écart est grand.
Un test statistique est souvent construit à partir d’un risque a, choisi à priori, par exemple 5%, avec lequel on calcule un seuil de rejet ou non de l’hypothèse, en fonction de la taille de l’échantillon.

• Si, dans le test, cette hypothèse alternative est explicitée, on peut, à partir du seuil p calculer le risque de seconde espèce b de rejeter cette hypothèse quand on n’est pas conduit à rejeter l’hypothèse principale.

• Un test statistique ne peut donc jamais conclure avec certitude, quand la vérification conduit à rejeter l’hypothèse, c’est avec un risque d’erreur inévitable, a de rejet à tort de l’hypothèse.
• Quand la vérification ne conduit pas à rejeter l’hypothèse, celle-ci ne se trouve pas pour autant validée : d’autres hypothèses, pourvu qu’elles ne soient pas trop différentes, pourraient également être validées.

Test graphique d’ajustement d’une distribution statistique à une loi de Gauss (droite de Henry)
Test graphique de Lilliefors
Test d’ajustement du c²
Test d’une fréquence
Test d’une moyenne
Test d’indépendance du c²

Retour en haut de la page

Autres fiches de statistique

Retour à la page d’accueil

Dernière mise à jour de cette page : 03 janvier, 2001 18:51:05.